土压平衡盾构始发与到达端头加固研究
江玉生1,江华1,2,潘茁1
(1.中国矿业大学(北京) 力学与建筑工程学院,北京 100083;2.中国矿业大学(北京) 深部岩土力学与地下工程国家重点实验室,北京 100083)
摘 要:为确保盾构始发与到达的顺利进行,避免施工过程中出现端头土体失稳现象,从而引发地表沉陷、塌方等工程事故,作者在分析了现有端头加固理论模型的优缺点后,基于端头加固土体的力学和数学模型,提出了基于强度理论的荷载等效模型和基于稳定性理论的砂性土端头滑动模型,给出了端头土体纵向加固范围计算公式。同时,根据盾构设备的几何构造特征及端头土体的渗透性要求,提出了盾构始发与到达端头土体纵向加固范围“几何准则”。该研究方法综合考虑了端头土体的强度、稳定性、渗透性及盾构设备的几何尺寸对盾构始发与到达的影响,研究结果对指导施工及反馈盾构隧道设计具有重要理论与实际意义,也可为类似研究提供参考。
关键词:盾构始发与到达;强度与稳定性;几何准则;端头加固
中图分类号: 文献标志码:A 文章编号:1009-7767(2012)02-0017-05
Research on Soil Improvement Scales at the Joint Areas of EPB TBM’s Launching and Break through
Jiang Yusheng1,Jiang Hua1,2,Pan Zhuo1
(1. School of Mechanics and Civil Engineering,China University of Mining and Technology,Beijing 100083,China;2.State Key Laboratory for GeoMechanics and Deep Underground Engineering, Beijing 10083,China)
Abstract:In order to keep the safety during TBM’s launching and break through and avoid larger ground settlement or collapses happening at the joint areas of TBM’s launching and break through, the relevant mechanical and mathematical models are established in this paper after making an detail analysis of advantages and disadvantages of current theoretical models for strata improvement at the joints areas. And the theoretical equations of tunnel longitudinal reinforcement scacles based on strength and stability theories are deduced. At the same time, according to geometrical characteristics of TBM and permeability requirement of improved strata, geometric principles along tunnel longitudinal improvement scales are also proposed. The methods adopted in this paper consider the influence induced by strength, stability, permeability of improved strata and the geometrical characteristics of EPB TBM, all these results are of not only theoretical and constructional importance for tunnel projects by EPB TBM, but also improving our tunnel design ideas and being referred for other similar studies.
Key words:launching and break through of EPB TBM; strength and stability; permeability; strata improvement
随着我国社会经济的快速发展和城市化进程的不断加快,城市人口聚集与城市地面交通基础设施落后之间的矛盾日益凸显,为了缓解这一矛盾,现代化的城市建设逐渐开始开发城市地下空间。城市地铁作为一种大容量的交通工具,逐渐受到人们的青睐,各大城市纷纷开始建设地铁。
盾构工法因其先进的施工工艺和不断完善的施工技术,以及适应多种地层和对地面扰动小的特点,在城市地下空间开发中取得了巨大的成功,并被越来越多地应用于城市地铁、市政管线共同沟等隧道工程的建设。但是,盾构工法在实际应用中还存在许多问题,如施工技术的稳定性不足,理论研究落后于工程实践,特别是盾构始发与到达,时有工程事故发生,事故原因大部分是由于端头土体失稳和地层渗漏所致,业已成为困扰盾构隧道施工的一大难题。
端头加固,是指盾构始发、到达以及盾构穿越已建风道、联络通道等既有建(构)筑物(相当于一次始发与到达过程)时,由于地层土体自稳能力较差而采取相应辅助工法对始发与到达端头区域工作井周围一定范围的土体进行改良加固的过程。近年来,随着我国许多城市纷纷开始建设城市地铁,盾构工法得到了空前的发展,但由于我国盾构施工技术起步较晚,尽管近几年投入了大量的人力、物力进行相关技术的研发、改进与提高以及人员的培训,但理论研究仍远远落后于工程实践,大多数工程问题仅依靠经验解决,没有形成完善的理论体系。因此,随着地层与环境条件愈发复杂,工程事故也不断增多。其中,端头失稳、透水等事故大多与土体加固范围不合理有关,纵向加固范围的确定问题已成为制约盾构始发与到达技术快速发展的关键工程问题之一。为了减少工程事故,确保盾构始发与到达施工的顺利进行,许多隧道及城市地下工程方面的专家和学者在基于强度与稳定性理论的端头加固模型、纵向加固范围的确定等方面进行了大量的研究。
日本学者较早开始了纵向加固范围的研究, 1990年日本JET GROUT协会(JJGA)利用弹性薄板理论,将端头土体受到的水土合力(梯形荷载)简化为均布荷载,推导得出了纵向加固范围计算公式。同时根据黏土地层的力学特征,给出了黏土地层端头土体几种可能的滑动模型,为纵向加固范围的稳定性验算提供了参考。
随着我国城市地铁工程的快速发展,张庆贺等国内学者将日本的荷载简化模型及端头滑移失稳模型引入中国并应用于我国地铁工程中[1-8]。
已有荷载简化理论模型和基于黏土的滑移失稳模型虽然在一段时间内在国内端头加固领域得到了较好的应用,但均是基于小直径盾构和单一性黏土地层提出的,随着盾构直径的不断增大以及端头地层条件的复杂化,已有荷载简化模型的计算结果应用于工程偏于危险且误差越来越大,稳定性模型仅仅适用于黏土,应用于其他类型地层时易引发工程事故。例如,南京地铁2号线盾构到达塌方、北京地铁大兴线盾构到达塌方及天津地铁2号线盾构始发塌方等事故都与设计加固范围不当、土体稳定性存在问题有关,造成了巨大的经济损失和不良的社会影响。
下面以土体的强度与稳定性理论为基础,分析盾构始发与到达端头土体的受力特征和力学模型,建立侧向梯形荷载的等效力学模型和砂土的滑移失稳模型,求得纵向加固范围计算公式,同时根据土压平衡盾构的几何构造特征和渗透性要求,提出了端头加固的“几何准则”。研究结果为将来类似问题的研究提供了参考。
1 强度及稳定性理论
1.1 已有理论模型
1)弹性薄板理论
已有弹性理论模型假设端头土体的纵向加固范围为t,洞门周边自由支撑的弹性圆形薄板为加固土体,如图1所示。将加固土体侧向水土合力的梯形荷载简化为均布荷载,在均布荷载的作用下,加固土体中心处的弯曲应力最大,由拉应力理论求得强度验算公式[7]:
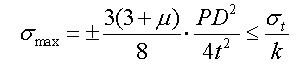 。(1)
。(1)
式中:D为洞门直径;t为纵向加固范围;P为作用于洞门中心处的侧向水土合压力;μ为加固土体的泊松比;σt为加固土体的极限抗拉强度;k为安全系数。
由均布荷载的作用特征可知,周边自由支撑的圆形薄板一周支座处的剪应力最大,由剪应力理论可得抗剪切强度的验算公式[7]:
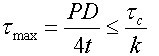 。 (2)
。 (2)
式中:τc为加固土体的极限抗剪强度。
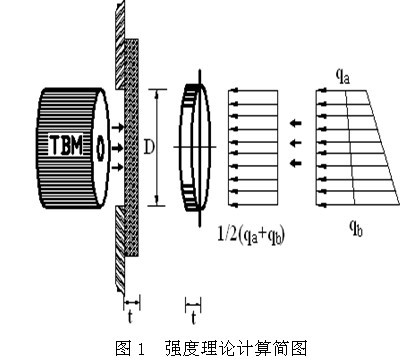
因此,根据静力学强度准则,端头土体加固后应同时满足抗拉和抗剪强度的要求,则端头土体的纵向加固范围应为:
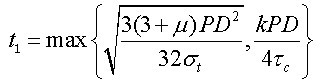 。(3)
。(3)
2)滑移失稳模型
盾构始发与到达施工时,破除洞门围护结构后掌子面土体完全暴露,至刀盘顶上围护结构之前有一定的时间间隔,此时10900.su,Guan Laitai.的叠加,即将e and Engineering,2008,4()le shield Departure Area.需要有一定端头土体在地面荷载、隧道上覆土体和侧向水土压力的共同作用下,可能沿着某个滑移面从开挖面向盾构工作井内滑动,发生滑移失稳破坏。目前,基于黏土的滑移失稳理论假定滑动面为以顶点O为圆心,洞径D为半径的圆弧面,如图2所示。
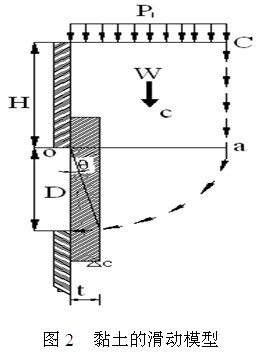
对于黏土地层,假设抗滑力矩完全由土体黏聚力提供,则由土体的平衡条件可知:KM=Md ,得出计算参数[7]:
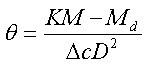 。 (4)
。 (4)
式中:M为滑动力矩;Md为抗滑力矩; Δc为改良后土体增加的黏聚力;K为抗滑安全系数;θ为加固土体与滑移面的夹角。
由几何知识可知,满足稳定性要求的纵向加固范围为[7]:
![]() 。 (5)
。 (5)
1.2 局限性分析
已有的理论模型对端头加固的强度与稳定性进行了分析,并给出了纵向加固范围的计算公式。从盾构工程端头土体的实际受力特征看来,已有的理论模型仍存在以下几点不足:
1)已有模型将端头土体受到的梯形荷载简化为均布荷载,简化后的荷载不能反映土体的真实受力情况,计算结果应用于实际工程时,偏于危险,特别是随着盾构直径与埋深不断变大,荷载简化误差将随之增大,容易引发严重工程事故。
2)滑移失稳模型只适用于黏土,对于无黏性土体的地层并没有给出具体的稳定性验算模型和公式,适用范围局限性较大。
1.3 改进的弹性理论模型
1)改进的强度理论模型
在分析和总结了已有模型的局限性后,作者根据弹性理论知识,对已有理论模型进行改进,建立了梯形荷载的等效力学模型,即将侧向梯形荷载等效为均布荷载和三角形反对称荷载的叠加,将非对称问题等效为一个对称问题和一个反对称的叠加,为盾构始发与到达端头土体纵向加固范围的研究提供了一条新的思路,力学模型如图3所示。
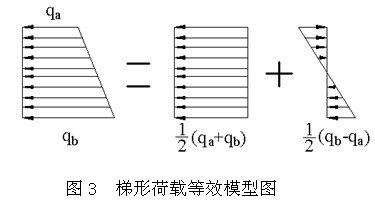
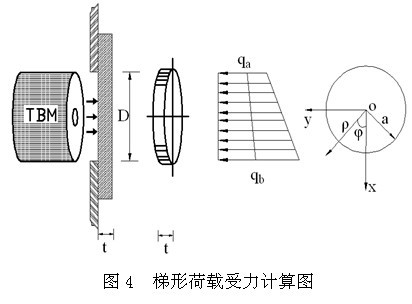
求解过程中首先对均布荷载和三角形反对称荷载作用下加固土体内力进行求解;然后通过内力叠加求出梯形荷载作用于端头加固土体的受力特征,同时利用加固土体的几何特征,求得端头加固土体受到的最大拉应力和最大剪应力;最后,根据加固土体的强度特征,利用最大拉应力及最大剪应力理论得出纵向加固范围[9-11]。
相关参数如图4所示[9-11]。同时满足抗拉和抗剪要求的纵向加固范围为:
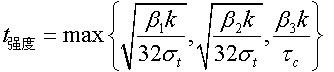 。(6)
。(6)
式中:σt为抗拉强度;τc为抗剪强度;β1,β2,β3为计算系数;k为安全系数。
1.4 改进的稳定性模型
砂土的破坏模式不同于黏性土体,因为砂土无内聚力。长久以来,世界各国的专家和学者在研究砂性土坡的破坏模式时,对砂性土坡的滑动进行了室内及室外模型实验研究[12-13],研究结果表明砂性土坡的破坏过程表现出突发性,其滑裂面从坡顶至坡脚形成一个近似直线型的滑裂面[14-15]。太沙基的松动土压力原理以及离心试验显示隧道顶板上方砂性土体的破坏面为近似的竖直滑动面,同时假设砂土地层洞门处破坏滑移面为斜直面,如图5所示。
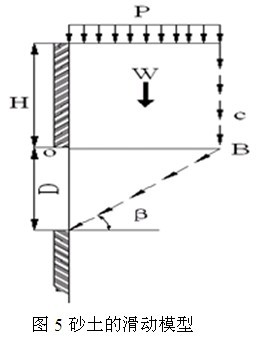
将砂性土坡的滑移破坏特性应用于盾构始发与到达端头加固的稳定性研究[9],当竖直土坡处于极限平衡状态时,潜在的破坏滑移面上滑动力与抗滑力处于静力平衡状态,求得稳定安全系数:
![]() 。 (7)
。 (7)
当FS=1时,β=φ ,则端头土体滑移范围:![]() 。根据抗滑要求,砂土的纵向加固范围:
。根据抗滑要求,砂土的纵向加固范围:
 。 (8)
。 (8)
式中:D为隧道洞门直径;φ为砂性土的内摩擦角。
2 渗透性理论及几何准则
砂层是一个力学不稳定地层,端头加固要求高,当地层中地下水丰富且压力较大时,端头加固不仅要满足强度与稳定性的基本要求,根据土压平衡盾构的构造特征,还必须满足堵水(渗透性)的要求。
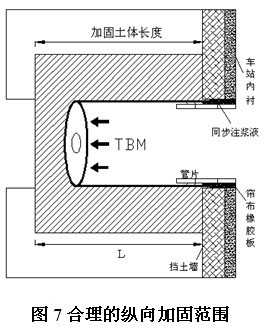
当地层有水或地层本身无水,但存在污水、上水管等有压管线(盾构施工时可能会出现管线破裂,水进入地层)时,考虑到地下水和砂可能沿着盾壳与地层之间的缝隙进入盾构工作井(如图6所示),造成涌水涌砂、地表沉降过大、塌方等工程事故,因此,为确保盾构始发与到达施工的安全,基于土压平衡盾构的几何构造特征,提出了端头土体加固的“几何准则”,即端头土体的纵向加固范围为:
L=盾构长度+(2~3)B , (9)
式中:B为管片的宽度,如图7所示。

3 结论
通过分析盾构始发与到达端头土体失稳的内在根源和力学机制,得出以下结论:
1)梯形荷载力学等效模型的建立,是得出考虑端头土体真实力学效应的纵向加固范围计算公式的基础,克服了现有计算公式的误差影响及其导致的工程危险性。
2)对黏土的滑移失稳模型进行改进,建立了砂土地层端头滑动破坏模型,为砂层端头加固的研究提供了参考。
3)基于土压平衡盾构的几何构造特征及端头加固土体的渗透性(止水)要求,提出了端头土体纵向加固“几何准则”。
参考文献:
[1]蒋洪胜,侯学渊. 盾构掘进对隧道周围土层扰动的理论与实测分析[J]. 岩石力学与工程学报,2003,22(9):1514-1520.
[2]赵峻,戴海蛟. 盾构法隧道软土地层盾构进出洞施工技术[J]. 岩石力学与工程学报,2004,23(2):5147-5152
[3]张庆贺,唐益群,杨林德. 隧道建设盾构进出洞施工技术研究[J]. 地下空间,1994,14(2):110-119.
[4]李大勇,王晖,王腾. 盾构机始发与到达端头土体加固分析[J]. 铁道工程学报,2006,1(2):87-90
[5]辛振省,王金安,马海涛,等. 盾构始发端欲加固合理范围[J]. 地下空间与工程学报,2007,3(6):513-518
[6]秦爱芳,李永和. 人工土层冻结法在盾构出洞施工中的应用[J]. 岩土力学,2004,25(S2):449-452.
[7]吴韬,韦良文,张庆贺. 大型盾构出洞区加固土体稳定性研究[J]. 地下空间与工程学报,2008,4(3):447-482.
[8]陈龙珠,陈胜立. 饱和地基上弹性圆板的动力响应[J]. 力学学报,2001,33(6):821-826.
[9]罗富荣,江玉生,江华. 基于强度与稳定性的端头加固理论模型及敏感性分析[J]. 工程地质学报,2011,19(3):364-369.
[10]Hua Jiang,Yusheng Jiang,Maolan Huang,et al. Study on Soil Improvement of TBM’S Commencement and Arrival in Water-rich Sand Stratum[J].Applied Mechanics and Materials, 2011,90(3):2119-2124
[11]Hua Jiang, Yusheng Jiang. Research on Mechanical Model and Scopes of Improved Strata at the Joint Areas of Large Diameter TBM’S Commencement and Arrival[C]//2011 International Conference on Technological Advancements in Civil Engineering,2011:101-105.
[12]Romo M P, Diaz M C. Face Stability and Ground Settlement in Shield Tunneling [C]//Soil Mechanics and Foundation Engineering Tenth International Conference. A.A.Balkema,1981:357-359.
[13]Chaffois S, Lareal P, Monnet J. Study of tunnel face in a gravel site[C]//Numerical Methods in Geomechanics.Swoboda,1988:1493-1498
[14]周小文,濮家骝,包承钢. 砂土中隧洞开挖稳定机理及松动土压力研究[J]. 长江科学院院报,1999,16(4):9-14.
[15]周小文,濮家骝. 砂土中隧洞开挖引起的地面沉降试验研究[J]. 岩土力学,2002,23(5):559-563.
收稿日期:2012-01-03
作者简介:江玉生,男,博士,副教授,主要从事盾构/TBM隧道技术研究工作。
注:本文刊载于《市政技术》2012年第2期,第17页至第20页。
