基于有限元模拟的双线平行盾构隧道近距离界定

    近年来，国内许多城市的地铁工程大多采用双线水平平行盾构施工，其引起的土体变形较大，尤其是地面沉降，会对周边环境和结构物产生潜在危害。目前，国内外对双线平行盾构施工引起的土体变形研究相对较少，研究方法主要有基于Peck公式的经验方法^[1-2]、随机介质理论^[3]、离心模型实验^[4-5]、 边界单元法^[6]、有限单元法^[7-8]和现场实测法。其中Peck公式法应用较多，有许多学者对Peck公式进行了进一步的研究，提出新的参数选择标准^[9-11]。研究表明：Peck公式能够准确地预测单线盾构隧道和双线水平平行盾构隧道近距离时引起的地面沉降，但双线水平平行盾构隧道的“近距离”界定目前尚无人研究。

    笔者提出了双线水平平行盾构隧道的相对水平距离系数C，采用三维有限元模拟，将双线平行盾构施工引起的地面沉降曲线与Peck公式相拟合，得到Peck公式的适用范围，对双线平行盾构隧道的“近距离”进行了界定。

1  双线水平平行盾构隧道近距离的界定

1.1  问题提出

    Peck ^[1]基于大量实测数据统计结果，认为土体移动由土体损失引起，在假定土体不排水、沉降槽体积等于土体损失体积的前提下，提出地面沉降槽呈拟正态分布，横向地面沉降估算公式为：

    ；     (1)

            。  (2)

式中：x为距隧道轴线横向水平距离；S(x)为x位置处的地面沉降量；S_max为隧道轴线上方最大地面沉降量；为单位长度土体损失量，，R为隧道开挖半径，为土体损失率；i为地面沉降槽宽度系数。以下公式符号同。

    Peck在1969年基于对芝加哥地铁双线隧道的研究，认为双线隧道引起的沉降槽也是对称分布的。Peck指出，由于后行隧道的开挖引起更大的土体损失，导致沉降槽宽度增加，但只有当沉降槽以两隧道中轴线为对称中心时，适合用Peck公式来描述双线隧道引起的沉降规律，在沉降槽计算中，用=R+L/2来代替R，来描述沉降槽宽度的增加，式中L为2条隧道轴线之间的水平距离。

但是当双线水平平行盾构隧道间距较远时，总的地面沉降曲线呈W形，此时Peck公式就不再适用。因此有必要对Peck公式的适用范围进行研究，即对双线水平平行盾构隧道的“近距离”进行界定。

1.2  研究现状及不足之处

    目前对于双线平行盾构隧道“近距离”的界定比较困难，大多采用有限元模拟，通过改变L来研究地面沉降曲线形状变化^[7-8]。

    令隧道轴线埋深为h，隧道外直径为D。韩昌瑞等^[7]研究表明：令h=3D，当L=2D时，地面沉降曲线符合正态分布；当L=3D时，曲线中间部位呈水平，不符合正态分布；当L=4D时，曲线呈W形状分布。Chehade等^[8]研究表明：令h=2.5D，当L=2D时，地面沉降曲线符合正态分布；当L>2D后，曲线不符合正态分布；当L=3D时，曲线呈W形状分布。但以上研究给出的近距离范围比较粗糙，且研究数据仅适用于其特定工况，需作进一步研究。

1.3  研究方法及思路

    分析认为，根据几何原理，双线水平平行盾构施工引起的地面沉降曲线形状应与地面沉降槽边缘点到隧道轴线的水平距离和L值有关，不能仅根据L值的大小来判断2条隧道是否为近距离。

如图1所示，图中阴影部分为双线隧道相互扰动区域。随着双线隧道间距由小到大，总的地面沉降曲线由“V”形向“W”形过渡；当隧道间距大于一定值时，其地面沉降曲线不符合正态分布，此时需使用其他较为复杂的公式来计算地面沉降。

 

 

    Cording等[12]经分析提出，对各种软塑到硬塑的黏土，地面沉降槽边缘点到隧道轴线的水平距离约为h+R。文献[13]的研究也表明该结论有一定可靠性。

    因此，笔者认为，双线平行盾构施工引起的地面沉降曲线形状与L和h+R有关。当L>h+R时，根据几何原理，双线平行盾构施工引起的地面沉降曲线会呈W形分布。令C=L/(h+R)，C为2条隧道轴线的相对水平距离系数。显然，C值越小，2条隧道的相对水平距离也越近。因此，可以用C值来界定双线水平平行盾构隧道的“近距离”。

笔者根据实际工程，考虑注浆液的硬化和L的改变，采用三维有限元模拟双线水平平行盾构隧道施工引起的地面沉降。将三维有限元模拟得到的地面沉降曲线与Peck公式相拟合，根据拟合程度，用C值来界定双线水平平行盾构隧道的“近距离”。

2  三维有限元模拟

2.1  模型建立

    定义土体为匀质黏土，本构模型采用莫尔-库伦模型，采用实体单元。隧道衬砌采用板单元，厚0.35m，采用C50混凝土，按线弹性材料考虑。隧道的h=12m，R=3.1m。在盾尾空隙中进行壁后注浆，注浆层宽0.07m，采用实体单元，按线弹性材料考虑，考虑到注浆液会随时间硬化，定义软注浆液和硬注浆液2种属性。材料的物理力学参数见表1。

 

 

 

    建立三维模型，设定土体的尺寸为横向80m，竖向40m，纵向70m。令土体每步开挖进尺为2m，隧道共划分为35段。盾壳与土体之间的摩擦力和开挖面支护力均假定为均布力，摩擦力和正面推力分别取45 kPa^[14]和138.9 kPa。注浆液硬化周期分为5步，由于注浆体是由液态逐渐硬化成固态，所以在盾构开挖过程中存在流动的软注浆液和硬化的硬注浆液。当注浆液硬化时不存在注浆力，故只在软注浆液阶段采用等效均布力来模拟盾尾同步注浆，取值为37kPa^[15]。图2为双线平行盾构隧道施工几何平面图，网格划分见图3和图4。

 

    三维有限元模拟步骤：1) 激活土体、自重荷载，位移清零，施加边界；2) 开挖土体；3) 激活衬砌，施加摩擦力和正面推力；4) 钝化盾尾注浆层，激活注浆液，施加注浆压力；5) 硬化注浆液，取消注浆压力。

2.2  改变隧道间距

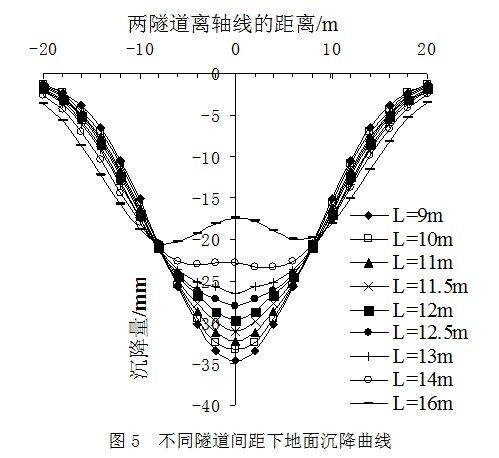
    改变图2中2条隧道轴线水平距离L，使其分别为9，10，11，11.5，12，12.5，13，14，16m，其他条件不变。模拟时令左侧隧道沿纵向掘进70m，右侧隧道沿纵向掘进68m，读取隧道始发处的地面沉降数据作为研究对象，此时该地面沉降曲线已经稳定，结果见图5。

    如图5所示，当2条隧道间距较小时，由于左右两侧隧道的相互影响较大，双线平行盾构隧道施工引起的地面沉降较大，沉降曲线基本呈轴对称，满足正态分布，可近似看成1个半径较大的单线盾构隧道开挖引起的地面沉降；随着L变大，由于左右两侧隧道的相互影响减小，双线平行盾构隧道施工产生的最大地面沉降逐渐减小，地面沉降曲线慢慢由V形转变成W形。

 

 

 

2.3  近距离的界定

    下面对图5中的地面沉降曲线进行详细分析，将模拟数据与Peck公式进行拟合，来研究Peck公式的适用范围。图6～12分别为L=9，10，11，11.5，12，12.5，13m时的三维有限元地面沉降模拟值与Peck公式计算值的拟合图。

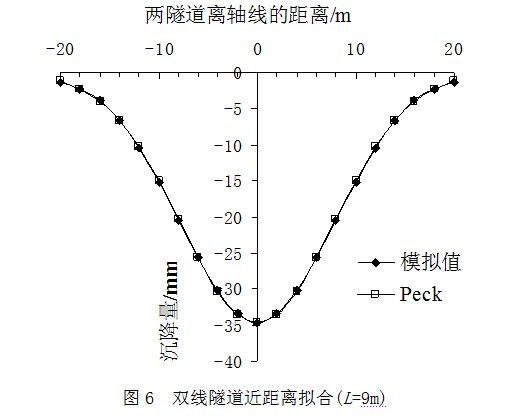
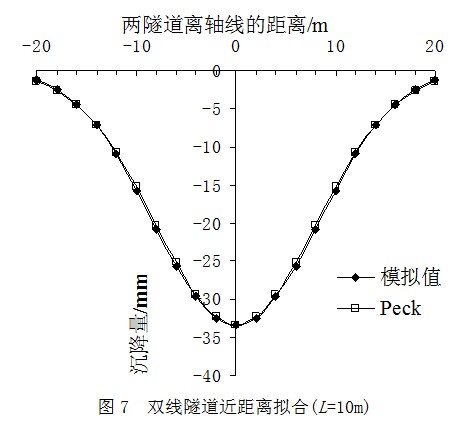
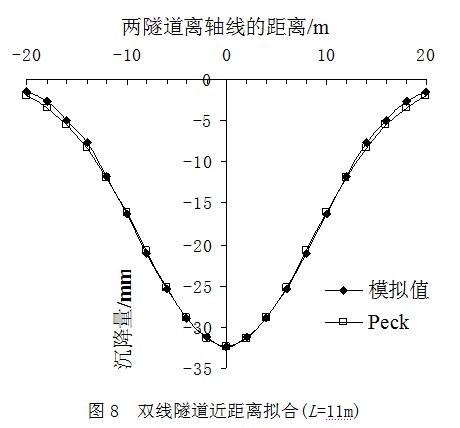
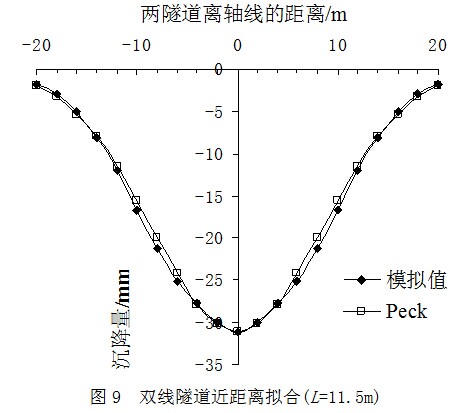
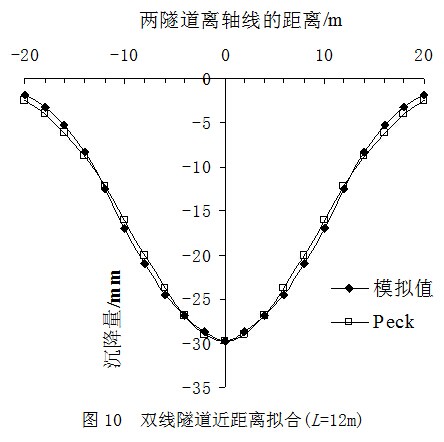
    如图6～12所示：当L=9m时，模拟值与Peck公式计算值十分吻合；当L=10m时，模拟值与Peck公式计算值也几乎完全重合，最大差异处只有0.5mm的误差；当L=11m时，模拟值与Peck公式计算值开始不吻合，在2条隧道距离中轴线6m的位置处沉降差异逐步增大；从L=11.5m至L=13m时，模拟值与Peck公式计算值之间的差异越来越大。可以看出，数据先在最外侧产生差异，后移向中轴线附近，最后整个区域的地面沉降都可看到明显差异。这表明随着L增大，两数值已明显不吻合。因此L=13m以后的数据笔者就不再重复拟合。

    由公式C=L/(h+R)，计算9组数据的C值，结果表明：当间距L为9，10，11，11.5，12，12.5，13，14，16m时，C值分别为0.59，0.66，0.73，0.76，0.79，0.82，0.86，0.92，1.05。

    由图6～12的拟合结果可知，当L=9m和10m时，地面沉降曲线符合正态分布规律；当L>10m后，地面沉降曲线均不符合正态分布规律。这是由于2条隧道相对距离过大的原因，与理论分析结果一致。因此笔者提出，令C=0.66作为双线水平平行盾构隧道近距离的界限，当C≤0.66时，适合采用Peck公式计算。

    下面采用韩昌瑞等^[7]和Chehade等^[8]人的研究数据，来验证以上结果的可靠性。韩昌瑞等^[7]研究表明：令h=3D，当L=2D时，地面沉降曲线符合正态分布，此时C=0.57；当L=3D时，曲线不符合正态分布，此时C=0.86，；当L=4D时，曲线呈W形分布，此时C=1.14。Chehade等^[8]研究表明：令h=2.5D，当L=2D时，地面沉降曲线符合正态分布，此时C=0.67；当L>2D后，曲线不符合正态分布，此时C>0.67；当L=3D时，曲线呈W形状分布，此时C=1。以上结果很好地验证了该研究结果的可靠性。

4  结论

    1) 当2条隧道近距离时，双线水平平行盾构隧道施工引起的总的地面沉降曲线符合正态分布规律，可以采用Peck公式计算；但随着水平距离的增大，地面沉降曲线不再符合正态分布规律，地面沉降曲线慢慢由V形转变成W形。

    2) 提出不能仅根据L值的大小来判断2条隧道是否为近距离，首次提出了相对水平距离系数C=L/(h+R)，即相对水平距离与L、h、R有关。可以采用C值来定量的界定2条隧道距离的远近。

    3) 将三维有限元模拟数据与Peck公式进行拟合，结果表明可令C=0.66作为双线水平平行盾构隧道近距离的界限。当C≤0.66时，适合采用Peck公式进行计算；当C>0.66时，Peck公式不再适用。该次研究中没有考虑隧道轴线埋深h和土质条件对地面沉降曲线的影响，可作进一步讨论。

 

注：本文刊载于《市政技术》20114年第1期，第76页至第80页。